Home List your patent My account Help Support us

Arterial stiffness measurement by ultrasound scanner

[Category : - HEALTH]
[Viewed 6557 times]

Abstract
The aim of this study is to introduce for the first time an innovative model allowing us to determine the 3-D arterial stiffness. Arterial stiffness is increasingly recognized as a predictor of cardiovascular
events but there is no method suited to calculate the arterial stiffness in 3-D. We measured 6 pairs of diameter, and diameter change of the right and the left common carotid artery of normal tension patients and their systolic and diastolic tensions. Then we calculate the arterial stiffness by introducing an hyper-elastic model in 3-D. Measurement of deformation of the common carotid artery on normal tension patients allows us to determine the average arterial stiffness of 474 kPa compared to 803 kPa recently published “Carotid and Aortic Stiffness : Determinants of Discrepancies ”, Stephane Laurent et als, Hypertension 47; 371-376 (Beaujon Hospital/Pr Leseche July 23, 2009). Our hyper-elastic
model takes into account the thickness and the incompressibility of the biological artery wall tissues.

Key Words : Arterial Stiffness, Compliance, Pulse Wave Velocity, Wall Thickness, Elasticity, Incompressibility, Hypertension, Hyper-elasticity, Diabetes, Smoking, Obesity and Overweight, Cholesterol, Aging.

1. Introduction
According to statistics from the World Health Organization (WHO), each year more than 17 million people die from cardiovascular disease (CVD), an estimated 31% of all deaths worldwide !
It is for these reasons that arteries gradually lose their elasticity and become more rigid than normal and that, without regular monitoring, even young people could be victims of CVD. We discovered about 20,000 people in Parisian region for 10 years
[1] although the blood pressure (BP) is normal, but the pulse pressure (PP) difference from the systolic pressure (Ps) to diastolic pressure (Pd) is abnormal, for example, 138/68 mmHg (138-68 = 70 mmHg is too wide, while the value Ps = 138 is always less than 140 mm and the value Pd = 68 mm less than 90 mm according to WHO
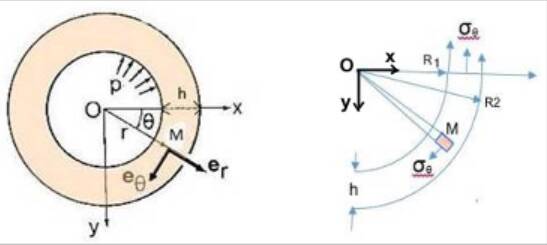
recommendations. However there is no 3-D method to determine AS precisely. We need to consider the value PP above, 6 pairs of diameter and thickness (h) (Fig.1) and 6 pairs of diameter and DC (Fig.2) to calculate AS by a hyper-elastic description [3-4] in a cylindrical coordinate system (Fig.5).

Fig.5. Cylindrical coordinate for a cross section

1. Introduction
According to statistics from the World Health Organization (WHO), each year more than 17 million people die from cardiovascular disease (CVD), an estimated 31% of all deaths worldwide !

It is for these reasons that arteries gradually lose their elasticity and become more rigid than normal and that, without regular monitoring, even young people could be victims of CVD. We discovered about 20,000 people in Parisian region for 10 years [1] although the blood pressure (BP) is normal, but the pulse pressure (PP) difference from the systolic pressure (Ps) to diastolic pressure (Pd) is abnormal, for example, 138/68 mmHg (138-68 = 70 mmHg is too wide, while the value Ps = 138 is always less than 140 mm and the value Pd = 68 mm less than 90 mm according to WHO recommendations. However there is no 3-D method to determine AS precisely. We need to consider the value PP above, 6 pairs of diameter and thickness (h) (Fig.1) and 6 pairs of diameter and DC (Fig.2) to calculate AS by a hyper-elastic description [3-4] in a cylindrical coordinate system (Fig.5).

2- Method and equipment

2.1 Equipment
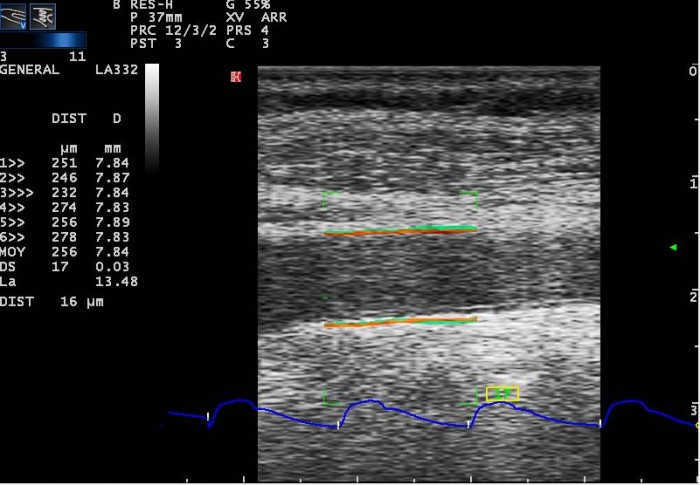
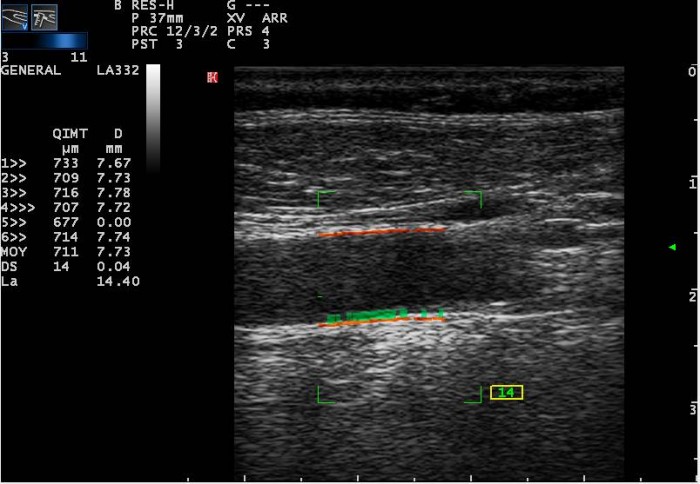
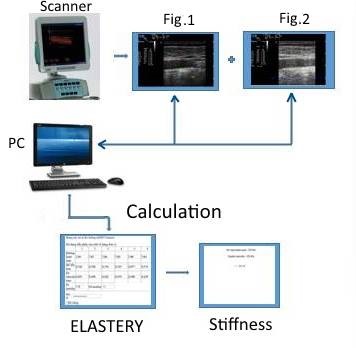
We start by measuring Ps (maximum systolic value), Pd (minimum diastolic value) and heart rate with an electronic blood pressure monitor, then we measure 6 pairs of thickness h = QIMT, diameter D (Fig.1) and the diameter change ?D = DIST (Fig.2) by an ultrasound scanner Esaote. Then the stiffness of the wall is automatically calculated (Fig.3)

2.2 Method
We collection 6 pairs (QIMT, D) (Fig.1) and (DIST, D) (Fig.2) of 3 measures done at the left and the right common carotid artery with the use of an ultrasound scanner equipped with a 7.5 MHz linear probe (MyLab Twice, Esaote France, HCM City, Vietnam). This setup anables the AS calculation together with blood pressure Ps, Pd will be performed automatically (Fig.3).

Fig.3. AS calculation by data acquisition from ultrasound scanner

The data saved (Fig.1&2) from the ultrasound scanner Esaote allow us to filling in 6 columns of the Elastery table and the software located in PC will automatically calculate AS coresponding to individual measure.

2.2 Method
We collection 6 pairs (QIMT, D) (Fig.1) and (DIST, D) (Fig.2) of 3 measures done at the left and the right common carotid artery with the use of an ultrasound scanner equipped with a 7.5 MHz linear probe (MyLab Twice, Esaote France, HCM City, Vietnam). This setup enables the AS calculation together with blood pressure Ps, Pd will be performed automatically (Fig.3).

Fig.1. (QIMT, D) measures of thickness and diameter
Fig.2. (D, DIST) measures of diameter and diameter change D=DIST

3- Results and discussion

3.1 Results
Measures are stored (Table 1) allowing us to calculate the arterial stiffness by a hyper-elastic equation of deformation and stress exerted on the wall, in a cylindrical coordinate system (Fig.5), with thickness h (QIMT) and invariable volume (Fig.8). We must determine the stress in the circumferential direction e? (Fig.6) of a cross section. The measures of normal hypertension patients are averaged summed and used for 3-D calculation EH=474 kPa.

Table 1 : Arterial measures

3.2 Discussion

We will compare AS determined by our 3-D hyper-elastic equation (stiffness EH=474 kPa, Table 1) with that published in a recent publication [2] Carotid Stiffness (CS) or Pulse Wave Velocity (PWV) = 7.79 m/s (Normal Tension, NT) (Table 2), 1-D stiffness E= 803 kPa (according to the Moens-Korteweg equation PWV² = Eh/D?), thickness h, diameter D and blood mass density ?=1058 kg/m3. The error committed by this classical equation is 70% in relation to 3-D hyper-elastic model.
Table

3.3 Histological analysis

1-D models

PWV pulse wave velocity [2]
It is calculated by PWV = L/?T, L is the length and ?T is the duration of the travel time and the stiffness (E, Einc,, YEM) deducted according to the Moens-Korteweg equation above while the 3-D stiffness value EH will be determined from a hyper-elastic model.

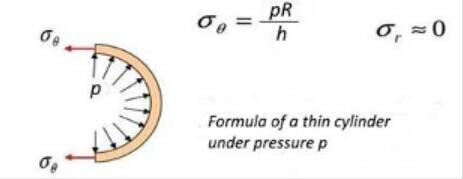
DC (Distension Coefficient) and CC (Compliance Coefficient) (Fig.5) are often used to determine AS of a 1-D equation, neglecting the thickness of the wall and according to the simple formula of a thin cylinder having negligible thickness h compared to D (h/D ? 0) (Fig.4)

Meinders and Hoeks formula (Fig.5) to calculate 1-D stiffness E, with the thickness h negligible (h/D ? 0) compared to D, h=QIMT (Fig.1). This formula in relation with PWV written as E=0.75(d/hDC) comes from the equation v² = (?²P/?t²).(?²P/?x²), that is to say approximately equal to A/? . (?A/?P) ? Eh/D? (Moens-Korteweg formula).

Fig.6. Stiffness formulas

Young, Peterson [5]
Round tube having for radius R (h/R ? 0), stress ? = E.? , ?P = EP.(?D/D) and the stiffness value of Peterson EP will be equal to EP = ?P.(D / Dd)

Incremental elastic modulus [6-9]
Thin cylinder (Fig.4) having radius R, diameter D and negligible thickness h (h/R ? 0), the stress in a circumferential direction of the surface of a cross section is equal to ? = ?P.R / h = ?P.D/2h because by definition ? = E.(?R/R) = ?P.D/2h and YEM (Young Elastic Modulus, Young Stiffness EY) will have as value YEM = ?P.D²/2h.?D which is an average value in the middle of the cross section thickness, or incremental elastic modulus Einc.

Note The formula E = 0.75 (D/h.DC) (Fig.5) is established in an incompressible medium with rigid wall, v² = (?²P/?t²).(?²P/?x²) , approximately equal to A/? (?A/?P) ? Eh/D? and written as D/h.DC (in addition to the coefficient 0.75), assuming the artery as a thin cylinder and negligible thickness compared to the diameter, h

Financial information

The patent rights will be sold because I as the inventor am not interested in handling the commercial side of the project. I can offer a venture start up company that could fund the patent and business development, but with my background as a Biomecanicien. The international rights is preseved by Registre canadien des droits d'auteur n° 480131.

Patent publications:

FR 2853519

Asking price:

Make an offer

Rate this patent

Great invention
Viewed: 6557 times

Seller:

stefan (France)

Seller's website

Ask a question
or start a negotiation

Contact the seller

Share on social media